Derivadas algebraicas: ejercicios explicados paso a paso

Una función polinómica, es una función conformada por monomios o polinomios, es decir, se encuentra estructurada por una serie de términos sumando o restando.

Con las funciones algebraicas se pueden realizar diversas operaciones entre las que se encuentra la derivada, que estudiaremos a continuación.

Derivadas algebraicas.

Se entiende por derivadas algebraicas, a la aplicación de los procesos o reglas de las derivadas para obtener la pendiente de la recta tangente en un punto determinado de una función algebraica.

Fórmulas para derivar funciones algebraicas

Para derivar funciones algebraicas así como otras funciones como las trigonométricas, funciones exponenciales, funciones logarítmicas, debemos conocer primero una serie de reglas básicas, que se encuentras resumidas en el formulario de derivada y que recordaremos a continuación:

Derivada de una constante: $\frac{d}{dx}C=0$
Derivada de la variable: $\frac{d}{dx}x=1$
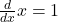
Derivada de una variable por una constante: $\frac{d}{dx}c.x=c.\frac{d}{dx}x=c.(1)$
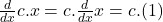
Derivada de una potencia: $\frac{\mathrm{d} }{\mathrm{d} x}x^{n}=nx^{n-1}$
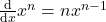
Derivada de una suma o resta: $\frac{\mathrm{d} }{\mathrm{d} x}[f(x)+g(x)+h(x)]=f'(x)+g'(x)+h'(x)$
Derivada de un producto: $\frac{\mathrm{d} }{\mathrm{d} x}u.v=u'.v+u.v'$
Derivada de un cociente: $\frac{\mathrm{d} }{\mathrm{d} x}\frac{u}{v}=\frac{u.v'-u.v'}{v^{2}}$

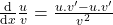
Ejercicios de derivadas de funciones algebraicas.

Vamos a resolver algunas derivadas algebraica:

Ejercicio 1.

$f(x)=9$

Solución

Como el diferencial corresponde a la variable x y la función a derivar es 9, se dice que es una constante por tanto el resultado es cero

$f(x)'=0$

Ejercicio 2.

$f(x)=x+5$

Solución

En este ejercicio tenemos dos términos sumando, por tanto se deben derivar ambos considerando que uno de ellos es una constante (5) y el otro termino esta elevado a exponente uno por tanto al derivar el resultado es 1

$f(x)'=1+0$

$=1$

Ejercicio 3.

$f(x)=x^{3}+x^{2}+x$

Solución

En este caso se deriva cada termino, se le restará uno al exponente, reflejándolo en esta oportunidad, pero el procedimiento se aplica de forma directa en la medida que logremos habilidad en la resolución de ejercicios.

$f(x)'=\ 3x^{3-1}+2.x^{2-1}+1$

$=\3x^{2}+2x+1$

Ejercicio 4.

$f(x)=\frac{6}{x^{4}}$

Solución

$f(x)'=\frac{x^{4}({6})\'-{x^{4}}\'(6)}{(x^{4})^{2}}$

$=\frac{x^{4}({0})-{4x^{3}}(6)}{x^{8}}$

$=\frac{-{24x^{3}}}{x^{8}}$

Simplificando los exponentes:

$=\frac{-{24}}{x^{5}}$

Solución alternativa: Nota que hemos calculado la derivada empleando la regla de la derivada de un cociente, si embargo, la función original podemos modificarla del siguiente modo:

$f(x)=6.x^{-4}$

Y de este modo, nos quedaría la derivada de una constante por una función (la potencia de exponente negativo) por lo que podemos calcularla del siguiente modo:

$f'(x)=6.(x^{-4})'$

$f'(x)=6.(-4)x^{-4-1}$

$f'(x)=-24x^{-5}$

Que es una expresión equivalente al resultado obtenido mediante el primer método, de hecho, esta es la forma habitual de calcular este tipo de derivadas.

Ejercicio 5:

$f(x) = \frac{1}{x^2} + 3x - 2$

Solución

Aplicamos la regla de la derivada de la suma y derivamos cada término individualmente:

$f(x) = (\frac{1}{x^2} )'+ (3x)' - 2'$

Hacemos la misma transformación que en el ejercicio anterior para derivar el primer término:

$f'(x) = (x^{-2})' + 3.1 - 0$ .

Calculamos la derivada de la potencia en el primer término y simplificamos:

$f'(x) = -2x^{-2-1} + 3$ .

$f'(x) = -2x^{-3} + 3$ .

Ejercicio 6:

$g(x) = \sqrt{x} + x^{\frac{3}{2}} - 2x^{-\frac{1}{2}}$

Solución

Derivamos cada término individualmente:

$g(x) = (\sqrt{x})' + (x^{\frac{3}{2}})' - (2x^{-\frac{1}{2}})'$

En el primer término tenemos una raíz cuadrada, que si bien podemos calcularla usando la regla de la raíz, también podemos calcularla convirtiéndolo en una potencia con exponente fraccionario y emplear la regla de la potencia, haciendo esto nos queda:

$g(x) = (x^{\frac{1}{2}})' + (x^{\frac{3}{2}})' - (2x^{-\frac{1}{2}})'$

Calculando las derivadas:

$g(x) = \frac{1}{2}x^{\frac{1}{2}-1} + \frac{3}{2}x^{\frac{3}{2}-1} - 2.(-\frac{1}{2})x^{-\frac{1}{2}-1}$

Simplificando:

$g(x) = \frac{1}{2}x^{-\frac{1}{2}} + \frac{3}{2}x^{\frac{1}{2}} +x^{-\frac{3}{2}}$

Puedes encontras más ejercicios de este y otro tema en nuestra publicación sobre ejercicios de derivadas