Tenemos claro que los limites indeterminados requieren de operaciones adicionales para obtener el valor del límite. Estas operaciones las estudiamos en la pagina de limites indeterminados, en esta ocasión nos dedicaremos a desarrollar algunos ejercicios para las indeterminaciones infinito entre infinito ![]() .
.
Contenido
- 1 Indeterminación infinito entre infinito
- 1.1 Ejercicios de limites indeterminados infinito entre infinito
- 1.2 Indeterminación cero entre cero
- 1.3 Indeterminación infinito menos infinito
- 1.4 Indeterminación uno elevado al infinito
- 1.5 Indeterminación cero por infinito (0.∞)
- 1.6 Indeterminación cero elevado a la cero
- 1.7 Indeterminación infinito elevado a la cero
Indeterminación infinito entre infinito 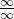
Para el caso de la indeterminación infinito entre infinito ![]() recordemos que debemos dividir el numerador y denominador por la variable de mayor exponente, simplificando posteriormente así finalmente se evalúa el límite.
recordemos que debemos dividir el numerador y denominador por la variable de mayor exponente, simplificando posteriormente así finalmente se evalúa el límite.
Al realizar este procedimiento se pueden presentas tres situaciones:
1.- Si la variable de mayor exponente se ubica en el numerador el resultado es infinito.
2.- Si la variable de mayor exponente se ubica en el denominador el resultado es cero.
3.- Si la variable de mayor exponente se ubica tanto en el numerador como denominador, el resultado sera la división de los coeficientes de dichas variables.
Es importante resaltar que durante las operaciones con infinito se pueden obtener los siguientes resultados:

Ejercicios de limites indeterminados infinito entre infinito 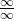
Resolver los siguientes ejercicios de límites:
Ejercicio 1.-
![]()
Solución
evaluamos
![]()
![]()
dividimos el numerador y denominador por la variable de mayor exponente siendo ![]() ;
;
![Rendered by QuickLaTeX.com \[=\displaystyle \lim_{x \to \infty }(\frac{\frac{x^{2}}{x^{2}}+\frac{3}{x^{2}}}{\frac{x}{x^{2}}})\]](https://calculodiferencial.com/wp-content/ql-cache/quicklatex.com-23aff41e0de9e0b04a007126398a23f3_l3.png)
![]()
evaluamos:
![]()
![]()
![]()
![]()
Ejercicio 2.-
![]()
Solución
si evaluamos
![]()
![]()
![]()
para eliminar la indeterminación dividimos el numerador y el denominador entre ![]()
![Rendered by QuickLaTeX.com \[=\displaystyle \lim_{x \to \infty }(\frac{\frac{2x^{3}}{x^{4}}+\frac{x^{2}}{x^{4}}}{\frac{x^{4}}{x^{4}}})\]](https://calculodiferencial.com/wp-content/ql-cache/quicklatex.com-00f2aa598695669f4b582688eb794146_l3.png)
![]()
![]()
evaluamos nuevamente
![]()
![]()
![]()
Ejercicio 3.-
![]()
Solución
si evaluamos tendremos como resultado ![]()
dividimos entre la variable de mayor exponente, siendo ![]()
![Rendered by QuickLaTeX.com \[=\displaystyle \lim_{x \to \infty }(\frac{2\frac{x^{5}}{x^{5}}-4\frac{x^{3}}{x^{5}}}{3\frac{x^{5}}{x^{5}}+\frac{2}{x^{5}}})\]](https://calculodiferencial.com/wp-content/ql-cache/quicklatex.com-7770f1cf0b9f066b31f5c6df053efc2e_l3.png)
![]()
evaluando;
![Rendered by QuickLaTeX.com \[=\frac{2-\frac{4}{(\infty )^{2}}}{3+\frac{2}{(\infty )^{5}}}\]](https://calculodiferencial.com/wp-content/ql-cache/quicklatex.com-4564ba85f98bbf65ed823dfdd73b578b_l3.png)
![]()
![]()
Otras publicaciones que te pueden interesar:
